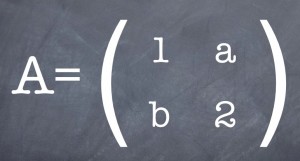頭に広がる無限の数 河東泰之

河東先生は生まれてから記憶がある限り、ずっと数学が大好きだったという。

中1のころには高校数学を自習し終え、数学の道を突き進んできた河東先生に数学の魅力を聞いてみた。

高校の数学、大学の数学

数学ができる人のイメージってどういったものでしょうか？

高校までの数学って計算が中心です。

複雑な計算が解ける人ができる人だと思われているし、テストなんかも複雑で難しい計算をさせる作りになっていたりします。

しかし大学の数学、研究者が研究している数学は違います。

数学者が研究している数学は、「なぜこうなるのか？」という基本原理を考えること。

計算ができる必要はあんまりなくって、研究とはそんなに関係ない。

計算が得意じゃない人もたくさんいます。

それよりも抽象的なコンセプトを考えることが大事になってきます。

テーマの選びかたも個々人が興味で選ぶことが多いです。

AさんとBさんの学説が対立する、といったことも少なくて、客観的にわかった／わからないという事実があるだけなんです。

私が好きなのは「無限」

私がいま研究しているのは作用素環論というジャンルです。

高校では数が横1列に並んだ数列を習います。

これが縦横2×2個並ぶと「行列」と呼びます。

高校数学ではせいぜい3×3の行列までしか出てきませんね。

では、この数字が縦にも横にも無限個並んだらどうなるでしょうか？

私は行列の数字が無限個並んだときに現れる性質について調べています。

無限個の要素をもつ行列どうしを比べたり、様々な理論がどう成立しているかなど行列に特有の性質を明らかにしたいと思っています。

わたしはこういったものすごく抽象的な世界が好きです。

行列の要素を有限（といっても数百万個など膨大）にしてあげると、応用物理学的なテーマに代わり、粒子論などに用いられる数学にかわります。

私もそうですが、数学者は抽象的なものは抽象的なまま、研究を突き進めていきます。

生きているうちに、物理学の世界で実験されるとは思っていませんし、そちらにはあまり興味がないんです。

ただ抽象的なままでよくて、これが世界中で研究するときにスムーズです。

なぜなら英語が下手でも、式を前にすれば一緒に考えられるからです。

年間の3分の1くらいは海外出張をしていますが、共同研究者たちと黒板に向きあって一緒に数学を考えるときは、とても創造的で、言葉の問題なんかほとんど感じません。

数学は理屈を理屈のまま考えることが好きなら、とても面白い学問なんです。

河東泰之先生よりメッセージ

河東泰之 Yasuyuki Kawahigashi

東京大学数理科学研究科

Written by Yusuke Shnozawa