自然界に「カズ」のきまりはあるのか? ロザン

「おもろふしぎラボ」は、よしもと芸人と科学大好きハカセが日常に潜むフシギを笑いをもって紹介する研究所です。今号、研究所を訪れたのは、ロザンのお2人です。

「おもろふしぎラボ」は、よしもと芸人と科学大好きハカセが日常に潜むフシギを笑いをもって紹介する研究所です。今号、研究所を訪れたのは、ロザンのお2人です。

宇治原

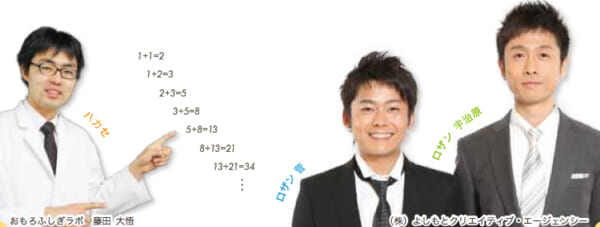
この間のクイズ番組でこんな問題が出たんですよ。「1、1、2、3、5、8、13、21、34、55…」この数列の名前はなに?

菅

そんなん簡単でしょ。答えは「整数」。

宇治原

そんなわけあるかい!これはな、フィボナッチ数列っていうんや。

菅

ミツバチハッチ?

宇治原

そうそう、「お母さんに会いたい!」ってちゃうわ!この数列は手前の2つの数字を足すと、次の数字になるわけや。1+1=2、1+2=3、2+3=5みたいな感じやな。この数列に含まれる数をフィボナッチ数っていうんやけど、じつは自然の中にたくさん見つかるらしいで。

菅

へー。たとえばどんなとこ?

ハカセ

たとえば花びらの数を650種類ほど調べると、92%がフィボナッチ数に当てはまったという調査結果があります。さらに、松かさやヒマワリの種子はよく見るとらせん状に並んでいますが、その巻き数を数えるとフィボナッチ数になっているんです。

菅

あんた誰?

宇治原

こら。この人はな、おもろふしぎラボのハカセや。でもハカセ、それって偶然なんじゃないんですか?

ハカセ

いや。植物の成長を、成長点の回転速度やひとつひとつの種子がつくられる時間間隔などの数字で表現してシミュレーションすると、フィボナッチ数になることが示されています。生き物のかたちを計算で表現できるって、おもしろいと思いませんか?

宇治原

へぇー。菅、理解できた?

菅

細かいところはようわからんけど、計算で生き物のかたちがわかるってのはおもろいなぁ。僕に何か足し算したら、背が伸びへんかな?

宇治原

さすがにそれはないやろ!